As we have seen, pitched notes are made up of many harmonic components, and it is possible to change the amplitude of those components without affecting the pitch that is perceived.  In 1964, R. Shepard devised a sequence of notes which continuously increased the perceived pitch without ever getting higher! Shepard tones are interesting in the sense that they only contain the octave components (or even multiples) of the frequency. Although our brain hears the pitch, it doesn't know where to place the fundamental frequency; this makes the tone ambiguous and this is why you hear an ever-ascending scale.

We have shown this subjective circularity in pitch judgement by generating a set of 12 complex tones sounded for 0.5 seconds and separated by a period of silence lasting 0.24 seconds. Each tone consists of 10 simultaneously sounded sinusoidal components spaced at octave intervals. The amplitudes of different frequency components are distributed in frequency as shown on the graph below. The bell-shaped curve forms a "spectral envelope".

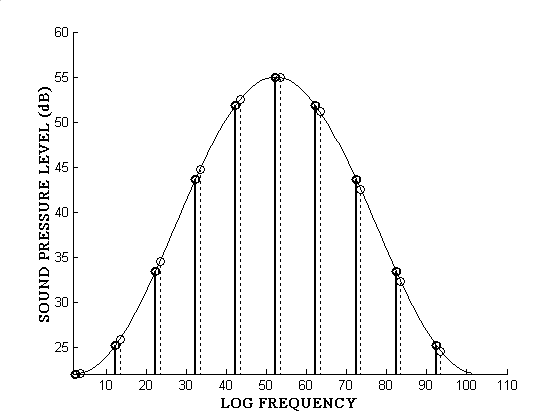
Illusions arise when the spectral envelope is held constant and the frequency components are increased or decreased in frequency. An increase in pitch  corresponds to an upward shift in the frequencies of all components as shown by the the dotted lines on the graph. This raising in pitch can be done in discrete steps as you can hear below:

This raising in pitch can also be done in a continuous fashion, thus creating a glide. This paradoxical sound is known as a Risset tone and can be heard below:

If you click on the blue buttons above, this should launch the Windows Media Player in  a separate window.