Standing waves may be created from two waves (with equal frequency, amplitude and wavelength) travelling in opposite directions. Using superposition, the resultant wave is the sum of the two waves. The animation below shows that the net result alternates between zero and some maximum amplitude. Unlike the travelling waves, the standing waves do not cause a net transport of energy (because the two waves which make them up are carrying equal energy in opposite directions).

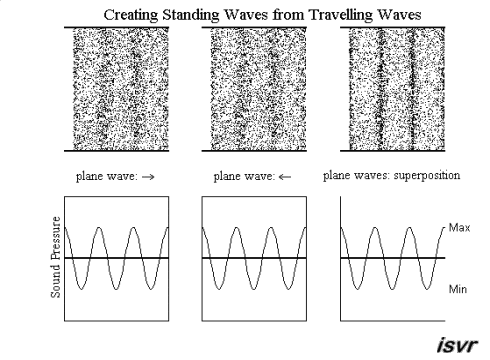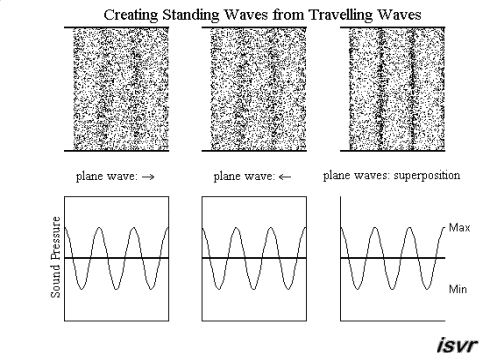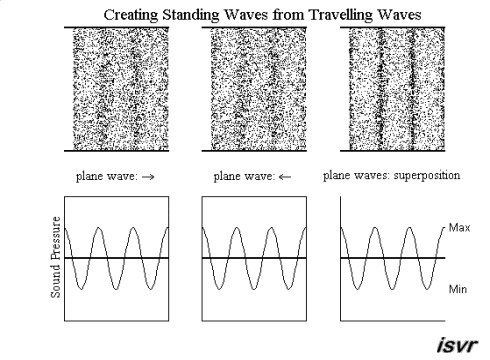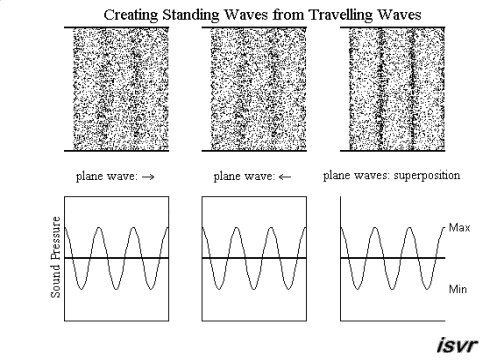
Notice that the particles right at the edge of the standing wave do not move. Points like this are called displacement nodes. This is what happens when an acoustic wave is reflected between two hard walls. The location where particle displacement is at a maximum is called a displacement antinode. Notice also that at a displacement node, the pressure variation is at a maximum, and so, a displacement node is also a pressure antinode. Similarly, a pressure node is also a displacement antinode.

It might be thought that it would be difficult to produce the two travelling waves that are identical except that they travel in opposite directions. However, this can readily be done using reflection and this is the case with many common systems for generating standing waves, as will be explained in the next section.