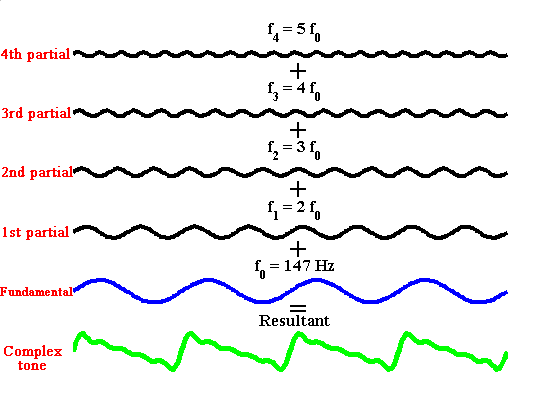
Musical notes are complex tones consisting of a fundamental frequency, f, and higher harmonics (or partials) that are integer multiples of the fundamental frequency (2f, 3f, 4f,...). The animation below shows the composition of a complex tone. The waveform of the fundamental is shown  (in blue) together with the waveform of the first four partials (in black) and the resultant complex tone (in green). The green waveform represents the fluctuation of the acoustic pressure with time produced at some location near a musical instrument. The relative amplitudes of the components are typical of the structure of the sound pressure fluctuation produced by a musical instrument. The mixture of tones determines the timbre of a musical instrument. In our example, the resultant pressure fluctuation, P_R, is the sum of the fundamental, P₁, and the first four harmonics, P₂, P₃, P₄, P₅, with appropriate amplitudes. In the case illustrated:

P₁ = sin ωt , P₂ = (1/2) sin 2ωt ,  P₃ = (1/3) sin 3ωt ,

P₄ = (1/4) sin 4ωt , P₅ = (1/5) sin 5ωt .

where ω = 2 π f  is the angular frequency. If we add more harmonics, the resultant will be a better approximation to a saw-tooth wave.

The pitch of a note is partly related to the fundamental frequency of the complex tone. We can now listen to a complex tone made up of a fundamental at 147 Hz and four higher harmonics. In musical language, this corresponds to the note D played in the first octave.

Let's now listen how a complex tone is modified after removing successively its lowest partials. Let's take the example of the note D. In the audio file, you can listen to the first tone composed of the fundamental plus four harmonics.

If you click on the blue button above, this should play the tone in a separate window.